Bellman-Held-Karp Hamiltonian path and Traveling Salesman

Figure below with mypaint and a Bamboo tablet on Ubuntu

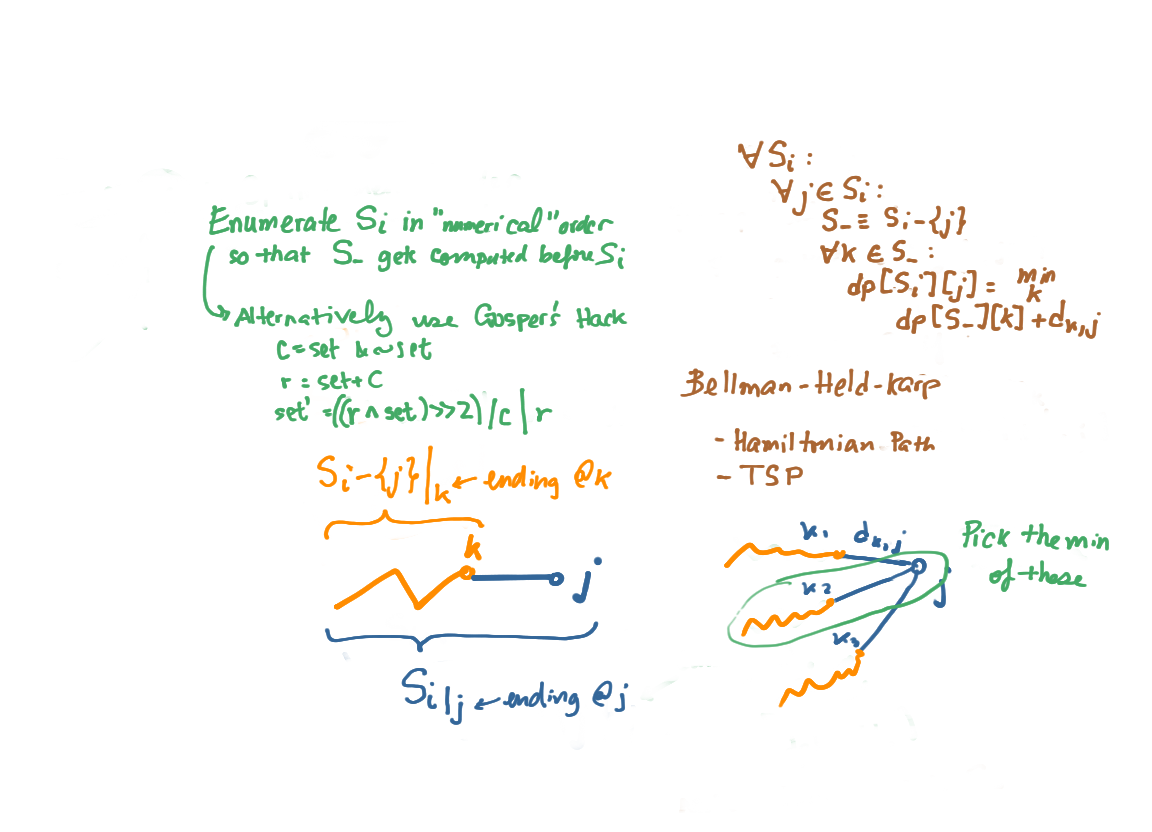
Floyd-Warshall connection

This section can be skipped, because it is basically my own brain mapping of this problem, since I feel there are some similarities with Floyd-Warshall.

For FW, I think of a source and destination pair \(i\) and \(j\) going through some intermediate node \(k\), and relaxing in a reverse triangle inequality kind of way, i.e.

\[ d[i][j] := \min(d[i][j], d[i][k] + d[k][j]) \]

From here it is not immediate obvious how to iterate, i.e. should the outer loop be over all \(i\) \(j\) pairs, or an outer loop over the intermediate node \(k\)?

This can be resolved by asking the question what do I need to know in order to compute \(d[i][j]\) at each step of the iteration. Since I depend on \(d[i][k]\) and \(d[k][j]\) it seems that I am going in a circle.

Instead think of the dp problem. What is the decision point, so that one can progress forward. Consider the decision point to be a source at a time, i.e. for a given source I will find all the best ways to reach a destination. This is kind of hard to achieve, since for a particular source, you also need to have information about the best source point from point \(k\) to \(j\), and this is not possible until we have reached the source iteration for element \(k\). By symmetry it should not be the destination point either.

Then let’s consider \(k\) as the decision point. In this case we consider all the savings going through \(k\) on a first pass. Then the next decision point will be \(k+1\) node, in which, we add another possible intermediate point, etc.

One way to graphically think about this is the following. When adding a single \(k\) you are looking at the best one or two segment routes. When adding the next \(k\) you are looking at the best one, two, three, or four segment paths. Because you can now go through another middle point.

There is a more formulaic expression which expresses this, which is helpful in capturing the dp nature of the problem:

\[ dp[i,j][k] = \min(dp[i,j][k-1], dp[i,k][k-1] + dp[k,j][k-1]) \]

Here \(k\) denotes two things in \(dp[i,k]\) it is the a source or destination, in \(dp[,][k]\) it denotes the set of decisions up to and including the \(k\) middle point. So it is saying that mid point \(k\) is now available, the best shortest path from \(i\) to \(j\) can be without considering \(k\) (\(dp[i,j][k-1]\)) or going through it (the RHS of the above).

Tie in with Bellman-Held-Karp

There is a similar consideration, but it is interesting to note the differences.

In BHK, we take into consideration a subset of the vertices, and compute the best possible paths from this subset that end at a particular vertex \(j\). Just as in the above, the dp formulation was considering all “\(k-1\)” solutions that don’t include the current decision \(k\). For the BHK case, it is considering all the \(S_i-\{j\}\) solutions that don’t include \(j\), to come up for the solution of \(S_i\) where \(j \in S_i\).

The other major difference is that the order in which \(k\) were considered in FW doesn’t matter, whereas in BHK, the order of \(S_i\) matters, as a matter of fact, one has to consider all possible subsets of \(S_i\) in order to solve for \(S_i\).

It is also interesting that the enumearation of subsets via binary bit representation in natural number order is a possible ordering of subsets, such that a later or larger number has dependencies that have been previously calculated. For example \(1001.0000\) only contains two elements, and its computation requires \(1000.0000\) and \(0001.0000\) both of which come earlier in numerical order. It is a little counter-intuitive that one is computing a two element subset so late in the enumeration. I think a more intuitive enumeration would be to consider all the 1 element subsets, followed by all 2 element subsets, etc. This can be done via Gosper’s hack. A clever bit manipulation technique that adds the LSB 1 to the number to get at the next subset of the same order.

Gosper’s hack sidetrack

c = set & ~set;
r = set + c;
set = ((r ^ set) >> 2) / c | r;

The first line gets the LSB that is set, then we add that to set in the second line to push the one forward. The last line takes care of the case where we cause a cascade of 1’s to flip, for example if we begin with \(0111.0000\) line two will flip all the ones in a row ending with \(1000.0000\). What we want at the end is to put two \(1\) at the beginning and end up with \(1000.0011\). This is accomplished by the xor and shift. The xor computes the number of digits that changed as a result of line two. The row of ones that got flipped will exactly contain \(1111\), showing all changes, which is two more than original number of bits. This is put at the beginning by shifting it back by the LSB location.

Hamiltonian path and TSP

The Hamiltonian path is equivalent to TSP, just think of the edges as being \(1\) or \(\infty\) weighed, and all the additions are capped at \(1\). Then we can find a Hamiltonian path if there exists a TSP solution.

Retaining the path

One way to retain the path, is keeping track of the parent for a particular \(S_i\) and \(j\). That is, when the if statement is taken then keep track of \(k\) which corresponds to a \(dp[S_-][k]\), or \(parent[S_i][j] = k\). Since we have \(S_i\) and \(j\) then we know \(S_- = S_i - \{j\}\), from which we can get its parent via \(parent[S_-][k]\) and so on.

Finding the TSP answer

The end result of BHK iteration is \(dp[S_{n-1}][j]\) array, which is the best path ending at \(j\). We need to consider all possible ending positions so the solution is the \(\min_j dp[S_{n-1}][j]\). Follow \(parent[S_{n-1}][j^*]\) to find the TSP path.

• Hamiltonian path
• traveling salesman
• Gosper's hack