ARTICLES
Bloom, count min sketch
By adam
Bloom
Probability of false positive
Probability that BF reports positive set membership for an element that is not in the set
\[ {\displaystyle \varepsilon =\left(1-\left[1-{\frac {1}{m}}\right]^{kn}\right)^{k}\approx \left(1-e^{-kn/m}\right)^{k}.} \]
\(k\) is the number of hash functions, \(m\) is the number of bits in the array, and \(n\) is the number of entries inserted into the table.
Obviously increasing \(m\) and decreasing \(n\) would decrease the \(\varepsilon\) however \(k\) has a optimal point.
Derivation
Probability that a certain bit is not set to 1 by a single hash function during insertion of an element.
\[ {\displaystyle 1-{\frac {1}{m}}} \]
Probability that the same bit is not set by the other \(k\) hash functions
\[ {\displaystyle \left(1-{\frac {1}{m}}\right)^{k}} \]
After inserting \(n\) elements, then the probably of not hitting is further reduced
\[ {\displaystyle \left(1-{\frac {1}{m}}\right)^{kn}\approx e^{-kn/m}} \]
This is for a single bit not being set.
The probability of it being set is \(1 - \{\}\). And raising it to the $k$th power gives \((1-\{\})^k\), one arrives at the probability of error given above.
Asymptotics and \(k\) for min \(\varepsilon\)
For large \(k\), the function goes to 1 and for \(k=1\) it goes to 1. Thus there is a minimum, obtainable from (just showing the exp approximation):
\[ \frac{d}{dx}\left(1 - e^{-k x}\right)^x = \frac{ \left(1 - e^{-k x}\right)^x \left(k x - \left(1 - e^{-k x}\right) \log\left(1 - e^{-k x}\right)\right)} {1 - e^{-k x}} \]
For the approx., \(k\) optimal is given by: \[ {\displaystyle k={\frac {m}{n}}\ln 2} \]
With minimum \(\varepsilon\), \[ {\displaystyle \ln \varepsilon =-{\frac {m}{n}}\left(\ln 2\right)^{2}} \]
Number of elements in a bloom filter
\[ {\displaystyle \left(1-{\frac {1}{m}}\right)^{kn}\approx e^{-kn/m}} \]
Recall the probabilty that a certain bit is not set, we can estimate the size of the set by counting the number of set bits \(X\)
\[ {\displaystyle \left(1-{\frac {X}{m}}\right) \approx e^{-kn/m}} \]
from which
\[ {\displaystyle n^{*}=-{\frac {m}{k}}\ln \left(1-{\frac {X}{m}}\right)} \]
With this one can do interesting counting, for example given the bloom fitler of \(A\) and \(B\) and \(A \cup B\) one can estimate the size of the intersection \(A \cap B\).
Count min sketch
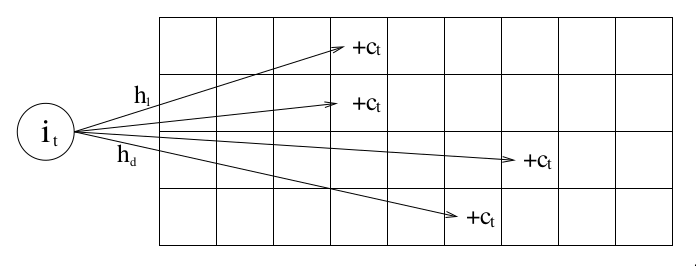
\(d\) hash functions \(h_j\), \(|j| = d\) (depth of the table)
\(w\) number of buckets (width of the table)
\(C(j,b) = C_j(b)\) a counter for each element in a stream.
CMS: \[ \hat{f_i} = \min_{j} C_j(h_j(i)) \]
\(m\) length of stream
Theorem
With a probability of
\[ {\displaystyle 1-\delta} \]
the error is at most
\[ \varepsilon || \text{stream} ||_1 \]
by setting
\[ w=\left \lceil \frac{e}{\varepsilon} \right \rceil \]
and
\[ d=\left \lceil \ln\frac{1}{\delta} \right \rceil \]
Proof
For a particular \(i\), and \(h_j\), and \(b = h_j(i)\),
\[ E[C_j(b)] = f_i + \frac{1}{w} \sum_{j \ne i: h_j(j)=b} f_j \le f_i + \frac{m}{w} \]
CMS only overestimates the count.
Using Markov’s inequality, and some more steps:
\[ Pr \{\hat{f_i} \ge f_i + \frac{2m}{w}\} \le \left( \frac{1}{d} \right)^d \]
Markov’s inequality
For non-negative RV a (a>0)
\[ {\displaystyle \operatorname {P} (X\geq a)\leq {\frac {\operatorname {E} (X)}{a}}} \]
Aside: nice proof:
\[ {\displaystyle \operatorname {E} (X)=\operatorname {P} (X<a)\cdot E(X|X<a)+\operatorname {P} (X\geq a)\cdot E(X|X\geq a)} \]
\[{\displaystyle E(X)\geq 0\cdot P(X<a)+a\cdot P(X\geq a)\geq a\cdot P(X\geq a)} \]
Hyperloglog
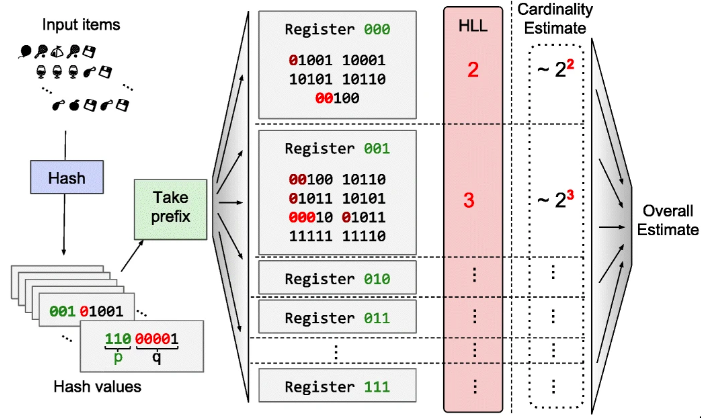
Durand and Flajolet

Heule, Nunkesser, and Hall

\[ {\displaystyle {\begin{aligned}x&:=h(v)\j&:=1+\langle x_{1},x_{2},..,x_{b}\rangle _{2}\w&:=x_{b+1}x_{b+2}…\M[j]&:=\max(M[j],\rho (w))\\end{aligned}}} \]
\(x\) for each element in stream