ARTICLES
Tree longest path by dfs 2x
By adam
Definition of a tree
(Taken from Wikipedia)
A tree is an undirected graph \(G\) that satisfies any of the following equivalent conditions:
-
\(G\) is connected and acyclic (contains no cycles).
-
\(G\) is acyclic, and a simple cycle is formed if any edge is added to \(G\).
-
\(G\) is connected, but would become disconnected if any single edge is removed from \(G\).
-
\(G\) is connected and the 3-vertex complete graph \(K_3\) is not a minor of \(G\).
-
Any two vertices in \(G\) can be connected by a unique simple path.
If \(G\) has finitely many vertices, say \(n\) of them, then the above statements are also equivalent to any of the following conditions:
-
\(G\) is connected and has \(n − 1\) edges.
-
\(G\) is connected, and every subgraph of \(G\) includes at least one vertex with zero or one incident edges. (That is, \(G\) is connected and 1-degenerate.)
-
\(G\) has no simple cycles and has \(n − 1\) edges.
Commentary
It is quite useful to understand each of these conditions. The interesting fact is that they are all equivalent definitions for a tree.
minor and complete graphs
There are a couple of interesting ones, in particular \(K_3\) cannot be a minor of \(G\). \(K_3\) is a fully connected graph with 3 vertices, which is essentially a cycle, and a minor is a cool concept of allowing deletion and contraction of edges, so saying that \(K_3\) is not a minor of \(G\) is equivalent to saying that \(G\) doesn’t have a cycle.
degeneracy
\(k\) -degenerate means that every subgraph (another graph containing a subset of vertices/edges of \(G\)) has vertices with degree at most \(k\). In particular the definition above says 1-degenerate, meaning that there is always a leaf or unconnected node in every subgraph of \(G\). This one is a little harder to understand, but it boils down to not having cycles. Because a subgraph with no vertices with 0 or 1 degree, implies that all vertices have degree of at least 2, i.e. there is a cycle.
Regarding DFS and longest path in a tree
I am not sure if this is the most concise way of proving this method:
-
From any leaf node find the furthest vertex from it.
-
From this vertex find the furthest vertex from it.
-
The path between the latter two vertices is a longest path in a tree.
Here is my proof, if you have a more concise proof, please share it.
I basically broke down the problem into two parts. Label the initial node as \(A\). Assume that the longest path is \(DC\) and that it is unique: there may be multiple equivalent longest paths, but for simplicity we will assume there is a unique longest path. We will prove that:
- the vertex furthest away from \(A\) cannot be some other node \(B\), it must be either \(D\) or \(C\) which are the endpoints of the longest path.
There are two possibilities for the path from \(A\) to \(B\) either it will intersect with the longest path \(DC\) (case I) or it will not (case II). We will consider each of these possibilities in turn.

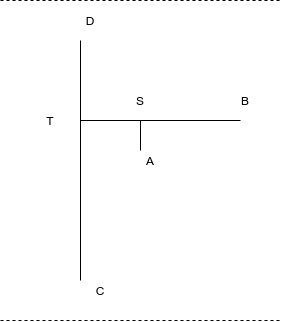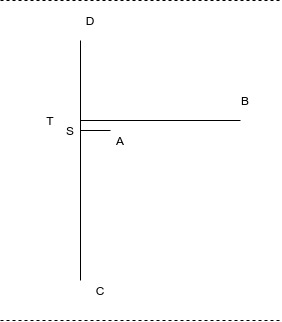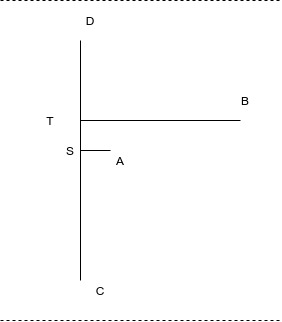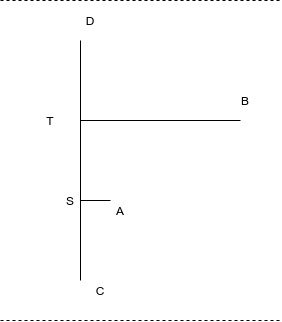
Case I
For this look at the left subfigure. Suppose \(AB\) is the longest starting at \(A\). If \(AB\) is the longest path from \(A\), this implies that \(TB > TD\), since the stub \(AS\) and \(ST\) are in common to both \(AD\) and \(AB\). If \(TB > TD\) this simplies that \(CTB > CD\) breaking our assumption that \(DC\) is the longest path. Thus \(B\) cannot be the node furthest away from \(A\).
Case II
For this look at the right subfigure. Suppose that \(AB\) is the longest path starting from \(A\). If \(AB\) is the longest path beginning at \(A\), this implies that \(AB\) > \(AD\). In particular this is saying that \(TB\) > \(TD\), since we can remove the stub \(AS\) as that is common between \(AB\) and \(AD\) and since \(SB > SD\) also implies that \(TB >TD\), by adding and subtracting \(ST\) from \(SB\) and \(SD\) respectively. If \(TB > TD\), then \(CTB > CTD\) which breaks our assumption that \(DC\) is the longest path.
Case I and II
I will note in passing that both cases are really the same case, if you allow the stub point \(S\) to move anywhere in the graph.
Conclusion
In the above, \(D\) and \(C\) can be interchanged. The analysis doesn’t really depend on their labels, just on their relative distance to the connections with \(A\). It might be simpler to consider a point \(S\) in case I and a point \(T\) in case II that lies in the middle of \(DC\).
Since there cannot be a point \(B \ne D\) or \(C\), then \(B\) must necessarily be either \(D\) or \(C\). Then if the furthest point from \(A\) is one of the endpoints in the longest path, either \(C\) or \(D\), then the furthest point from one of these two endpoints will be the other corresponding vertex in the longest path by our assumption of longest path.